Ο Monty Hall είναι Καναδός τηλεπαρουσιαστής , που παρουσίαζε το περίφημο τηλεπαιχνίδι Let’s make a deal στο ABC από το 1963 μέχρι το 1977 και σε μερικές ακόμα μεμονωμένες σαιζόν μέχρι και το 1991.
Όμως αν κάποιος «χτυπήσει» στο google το ονομα Monty Hall δεν θα έχει αποτέλεσμα τον παρουσιαστή αλλά ένα από τα μεγαλύτερα παράδοξα της επιστήμης των Πιθανοτήτων.
Όλα ξεκίνησαν όταν το 1975 ο Steve Selvin έστειλε ένα γράμμα στο περιοδικό American Statistician, δημοσιεύοντας ένα πρόβλημα βασισμένο στο συγκεκριμένο τηλεπαιχνίδι, το οποίο αργότερα ονόμασε Monty Hall problem, .Το Monty Hall problem έχει ως εξής.
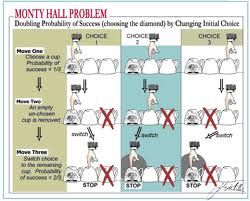
Πίσω από τρεις κουρτίνες τοποθετούνται ένα αυτοκίνητο και δύο κατσίκες. Ο παρουσιαστής γνωρίζει ποια κουρτίνα κρύβει το αυτοκίνητο. Ο παίκτης καλείται να επιλέξει μια κουρτίνα, π.χ. την Α. Στη συνέχεια ο παρουσιαστής ανοίγει μία από τις άλλες κουρτίνες που κρύβει πίσω της μία κατσίκα. Ας πούμε ότι ανοίγει τη Β. Δίνεται τώρα στον παίκτη η δυνατότητα είτε να επιμείνει στην αρχική επιλογή του(κουρτίνα Α) είτε να αλλάξει και να ανοίξει την κουρτίνα Γ. Τι έχει συμφέρον να κάνει ο παίκτης;
Η πρώτη απάντηση που έρχεται στο μυαλό των περισσοτέρων είναι ότι αφού έχει ήδη ανοίξει μία κουρτίνα που έκρυβε κατσίκα και έχουν απομείνει μία κουρτίνα με κατσίκα και μία με το αυτοκίνητο, οι πιθανότητες είναι πια 50-50 και καμιά από τις δυνατές επιλογές του παίκτη δεν είναι ευνοϊκότερη από την άλλη. Εικασία η οποία αποδεικνύεται λάθος!
Για να κατανοήσουμε το γιατί πρέπει να σκεφτούμε ποιες είναι δυνατές στρατηγικές που θα ακολουθησει ο παίκτης τη όταν μπει στο στούντιο: Υπάρχουν δύο επιλογές :
1η Ο παίκτης επιλέγει μία κουρτίνα π.χ. την Α) και εμμένει σε αυτήν μέχρι το τέλος, ό,τι και αν του πει ο παρουσιαστής. Αφού υπάρχουν τρεις κουρτίνες και ένα αυτοκίνητο, η πιθανότητα νίκης με αυτή τη στρατηγική είναι 1/3.
2η Ο παίκτης επιλέγει αρχικά μία κουρτίνα (π.χ. την Α) και μόλις ο παρουσιαστής ανοίξει μία άλλη κουρτίνα (π.χ. τη Β) και αποκαλύψει μία κατσίκα, αλλάζει και επιλέγει την κουρτίνα Γ που έχει απομείνει.
Με αυτή τη στρατηγική, ο παίκτης για να κερδίσει τελικά οφείλει να επιλέξει αρχικά μία κουρτίνα με κατσίκα. Ο παρουσιαστής θα ανοίξει τότε την άλλη κουρτίνα με την κατσίκα και αλλάζοντας ο παίκτης θα πάρει τελικά το αυτοκίνητο. Έτσι η πιθανότητα νίκης του με αυτή τη δεύτερη στρατηγική είναι 2/3.
Είναι γεγονός ότι μαθηματικοί μεγάλου βεληνεκούς, δεν βρίσκουν τη σωστή απάντηση. Είναι πολύ γνωστή η διένεξη της Μεριλιν Φος Σαβαντ του ανθρώπου εν ζωή με το με μεγαλύτερο IQ (228 μονάδες) με πολλούς μαθηματικούς. Η Μεριλιν Φος Σαβαντ έγραφε μια δημοφιλή στήλη στο περιοδικό parade η οποία τιτλοφορούνταν «ρώτα την Μεριλιν».Το 1990 όταν ρωτήθηκε για το παράδοξο του Monty Hall από αναγνώστη του περιοδικού υποστήριξε ότι να βελτιωθούν οι πιθανότητες πρέπει ο διαγωνιζόμενος οπωσδήποτε να αλλάξει κουρτίνα. Το αποτέλεσμα ήταν απρόσμενο 10000 αναγνώστες από τους οποίους οι 1000 είχαν τριτοβάθμια εκπαίδευση έστειλαν διαμαρτυρία στο περιοδικό ότι η λύση ήταν λανθασμένη. Η Μεριλιν Φος Σαβαντ τελικά δικαιώθηκε . Η απάντηση της επαληθευτικέ πειραματικά με την μέθοδο Montecarlo . Οι στατιστικές δείχνουν ότι μόλις το 13% των ανθρώπων απαντάει σωστά στην παραπάνω ερώτηση.

ΔΟΚΙΜΑΣΤΕ ΟΛΑ ΤΑ ΣΥΣΤΗΜΑΤΑ ΔΩΡΕΑΝ ΣΕ ΑΛΗΘΙΝΟ ΟΝΛΙΝΕ ΚΑΖΙΝΟ
Όμως αν κάποιος «χτυπήσει» στο google το ονομα Monty Hall δεν θα έχει αποτέλεσμα τον παρουσιαστή αλλά ένα από τα μεγαλύτερα παράδοξα της επιστήμης των Πιθανοτήτων.
Όλα ξεκίνησαν όταν το 1975 ο Steve Selvin έστειλε ένα γράμμα στο περιοδικό American Statistician, δημοσιεύοντας ένα πρόβλημα βασισμένο στο συγκεκριμένο τηλεπαιχνίδι, το οποίο αργότερα ονόμασε Monty Hall problem, .Το Monty Hall problem έχει ως εξής.
Πίσω από τρεις κουρτίνες τοποθετούνται ένα αυτοκίνητο και δύο κατσίκες. Ο παρουσιαστής γνωρίζει ποια κουρτίνα κρύβει το αυτοκίνητο. Ο παίκτης καλείται να επιλέξει μια κουρτίνα, π.χ. την Α. Στη συνέχεια ο παρουσιαστής ανοίγει μία από τις άλλες κουρτίνες που κρύβει πίσω της μία κατσίκα. Ας πούμε ότι ανοίγει τη Β. Δίνεται τώρα στον παίκτη η δυνατότητα είτε να επιμείνει στην αρχική επιλογή του(κουρτίνα Α) είτε να αλλάξει και να ανοίξει την κουρτίνα Γ. Τι έχει συμφέρον να κάνει ο παίκτης;
Η πρώτη απάντηση που έρχεται στο μυαλό των περισσοτέρων είναι ότι αφού έχει ήδη ανοίξει μία κουρτίνα που έκρυβε κατσίκα και έχουν απομείνει μία κουρτίνα με κατσίκα και μία με το αυτοκίνητο, οι πιθανότητες είναι πια 50-50 και καμιά από τις δυνατές επιλογές του παίκτη δεν είναι ευνοϊκότερη από την άλλη. Εικασία η οποία αποδεικνύεται λάθος!
Για να κατανοήσουμε το γιατί πρέπει να σκεφτούμε ποιες είναι δυνατές στρατηγικές που θα ακολουθησει ο παίκτης τη όταν μπει στο στούντιο: Υπάρχουν δύο επιλογές :
1η Ο παίκτης επιλέγει μία κουρτίνα π.χ. την Α) και εμμένει σε αυτήν μέχρι το τέλος, ό,τι και αν του πει ο παρουσιαστής. Αφού υπάρχουν τρεις κουρτίνες και ένα αυτοκίνητο, η πιθανότητα νίκης με αυτή τη στρατηγική είναι 1/3.
2η Ο παίκτης επιλέγει αρχικά μία κουρτίνα (π.χ. την Α) και μόλις ο παρουσιαστής ανοίξει μία άλλη κουρτίνα (π.χ. τη Β) και αποκαλύψει μία κατσίκα, αλλάζει και επιλέγει την κουρτίνα Γ που έχει απομείνει.
Με αυτή τη στρατηγική, ο παίκτης για να κερδίσει τελικά οφείλει να επιλέξει αρχικά μία κουρτίνα με κατσίκα. Ο παρουσιαστής θα ανοίξει τότε την άλλη κουρτίνα με την κατσίκα και αλλάζοντας ο παίκτης θα πάρει τελικά το αυτοκίνητο. Έτσι η πιθανότητα νίκης του με αυτή τη δεύτερη στρατηγική είναι 2/3.
Είναι γεγονός ότι μαθηματικοί μεγάλου βεληνεκούς, δεν βρίσκουν τη σωστή απάντηση. Είναι πολύ γνωστή η διένεξη της Μεριλιν Φος Σαβαντ του ανθρώπου εν ζωή με το με μεγαλύτερο IQ (228 μονάδες) με πολλούς μαθηματικούς. Η Μεριλιν Φος Σαβαντ έγραφε μια δημοφιλή στήλη στο περιοδικό parade η οποία τιτλοφορούνταν «ρώτα την Μεριλιν».Το 1990 όταν ρωτήθηκε για το παράδοξο του Monty Hall από αναγνώστη του περιοδικού υποστήριξε ότι να βελτιωθούν οι πιθανότητες πρέπει ο διαγωνιζόμενος οπωσδήποτε να αλλάξει κουρτίνα. Το αποτέλεσμα ήταν απρόσμενο 10000 αναγνώστες από τους οποίους οι 1000 είχαν τριτοβάθμια εκπαίδευση έστειλαν διαμαρτυρία στο περιοδικό ότι η λύση ήταν λανθασμένη. Η Μεριλιν Φος Σαβαντ τελικά δικαιώθηκε . Η απάντηση της επαληθευτικέ πειραματικά με την μέθοδο Montecarlo . Οι στατιστικές δείχνουν ότι μόλις το 13% των ανθρώπων απαντάει σωστά στην παραπάνω ερώτηση.
ΔΟΚΙΜΑΣΤΕ ΟΛΑ ΤΑ ΣΥΣΤΗΜΑΤΑ ΔΩΡΕΑΝ ΣΕ ΑΛΗΘΙΝΟ ΟΝΛΙΝΕ ΚΑΖΙΝΟ
Tags:
ΠΙΘΑΝΟΤΗΤΕΣ ΟΔΗΓΟΣ